
I DECIBELS
Decibels
Questa sezione è dedicata ad un argomento che spesso risulta un pò ingarbugliato in quanto le definizioni sono molte e si corre il rischio di scambiare una cosa per l'altra.
Eppure il concetto di decibel è alla base della teoria del suono e ricompare sistematicamente ogni volta che ci troviamo a misurare una grandezza ad esso collegata. Il motivo di tale importanza risiede nel fatto che l'orecchio umano percepisce la pressione sonora in maniera logaritmica anziché lineare e dunque risulta conveniente esprimere le grandezze legate all'ampiezza del suono in un'unità di misura logaritmica: il decibel.
La scala logaritmica
Una scala descrive il rapporto tra due grandezze. La scala logaritmica si differenzia dalla scala lineare per il fatto che la proporzionalità tra le due grandezze non è costante ma ha un andamento appunto logaritmico. La tabella seguente evidenzia la diversa corrispondenza tra due grandezze X e Y legate da una relazione lineare e logaritmica:
Confronto tra scala lineare e scala logaritmica
| SCALA | LINEARE | SCALA | LOGARITMICA |
|---|---|---|---|
| X | Y | X | Y |
| 1 | 1 | 1 | 10 |
| 2 | 2 | 2 | 100 |
| 3 | 3 | 3 | 1000 |
| n | n | n | 10n |
Il decibel relativo ad una grandezza X generica viene espresso nella forma:

che misura la variazione in decibel della grandezza rispetto ad un valore di riferimento fissato X0 Se per esempio lagrandezza che consideriamo è la X e il nostro valore di riferimento è X0=10, passando da X0 a X=1000 otteniamo un incremento in dB espresso dalla formula seguente:

I decibels Audio
La grandezza che si incontra più comunemente è il dBspl (spl: sound pressure level, livello di pressione sonora) che viene definito come:

in cui P0 è il valore di riferimento per la pressione atmosferica e viene preso pari a 0.00002Pa = 20 μPa(la pressione viene misurata in Pascal) che viene considerata la pressione sonora al di sopra della quale l'orecchio umano comincia a percepire un suono.
Vediamo un esempio. Il valore di 20 μPa è un valore di riferimento per la pressione sonora in un ambiente in assenza di onde acustiche.
Ciò significa che una pressione sonora di 20 μPa non esercita nessuna pressione sonora percepibile dall'apparato uditivo. Viceversa una pressione sonora di 10Pa genera un certo numero di dBspl pari al risultato seguente:

Leggendo la formula in un altro modo possiamo dire che una pressione sonora di 114dBspl corrisponde ad un'onda acustica che sviluppa una pressione di 10 Pa. La seguente figura illustra dei tipici suoni e la loro intensità espressa in dBspl:

Legge della distanza inversa
È una legge empirica che ci serve per calcolare la variazione di dBspl al variare della distanza da una sorgente sonora. Se ad una distanza d1 dalla sorgente sonora misuriamo una pressione sonora di dBspl1, ad una distanza d2>d1 avremo una pressione sonora data dalla formula:

Vediamo un semplice esempio pratico: se d1 = 1m e a questa distanza dalla sorgente sonora misuriamo dBspl1=100 avremo alla distanza d2=2m una pressione sonora pari a:

Da questo semplice esempio ricaviamo una comodissima regola empirica, ogni volta che ci allontaniamo dalla sorgente sonora raddoppiando la distanza riscontriamo una caduta pari a 6 dBspl , viceversa se ci avviciniamo dimezzando la distanza percepiamo una aumento della pressione sonora di circa 6 dBspl.
Tale regola prende appunto il nome di legge della distanza inversa.
Combinazioni di sorgenti sonori
Quando vengono combinate più sorgenti sonore, ognuna delle quali genera una certa quantità di dBspl non è possibile sommare semplicemente questi valori ma bisogna utilizzare la formula empirica seguente:

Vediamone un esempio considerando due sorgenti sonore uguali di 90dBspl.
Avremo:

Anche da questo esempio ricaviamo una importante regola empirica: sommando due sorgenti sonore uguali si ottiene un incremento di 3dBspl (e non un valore pari al doppio!). Dunque se abbiamo un impianto P.A. (Public Address).
“È il sistema di altoparlanti deputato alla diffusione del suono in una sala”.
Che produce una pressione acustica di 100dBspl, aggiungendo un secondo impianto analogo otterremo una pressione acustica complessiva pari a 103dBspl; per arrivare a 106 dBspl dovremo aggiungere altri due P.A. e arrivare a quattro e così via.
Grandezze elettriche espresse in decibel
Dato che il dB riproduce la percezione delle grandezze sonore da parte dell'orecchio umano, sono espresse in dB anche una serie di grandezze elettriche che vengono impiegate nella pratica. Di seguito diamo conto delle più utilizzate.
Inizialmente usato per misurare i rapporto di potenza sulle linee telefoniche. Generalmente i circuiti adibiti a questo scopo avevano un'impedenza [Impedenza] di 600Ω. Come valore di riferimento veniva preso 1mW da cui:

Da questa formula possiamo ricavarne una equivalente in cui compaiono tensioni al posto di potenze. Sostituendo infatti la formula:

e ponendo: "R1 = R2 "
Otteniamo la seguente:
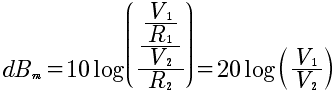
(Come si vede, nella formula per ricavare il valore dei dB a partire dalla tensione, il fattore moltiplicativo del logaritmo è ora pari a 20. Dunque nel caso di potenze abbiamo un fattore pari a 10, nel caso di tensioni il fattore vale 20.)
Questo valore è stato introdotto per la necessità di dover considerare corcuiti con impedenze diverse da 600Ω. La 'u' di dBu indica dunque che il valore è di tipo 'unloaded' cioè indipendente dall'impedenza. Per il calcolo del dBu il carico viene inglobato all'interno di una tensione di riferimento che si ottiene dal calcolo seguente:

da cui:

Questa tensione dunque ingloba una potenza di riferimento pari a 1mW e una resistenza di riferimento pari a 600Ω.
La formula finale per il calcolo del dBu è la seguente:

Equazione dBu:
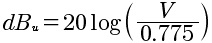
In questo caso il voltaggio di riferimento viene preso pari a 1 Volt dunque si usa la formula:
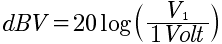
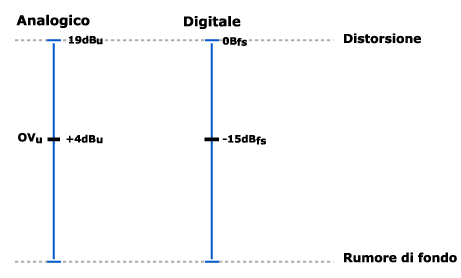
La scala dB digitale è leggermente diversa. Anzitutto l'unità di misura è il dBfs e il valore più alto è sempre 0 dBfs. Oltre questo valore si ha distorsione digitale. Il suono della distorsione digitale risulta molto diverso da quello della distorsione analogica e inoltre la distorsione analogica aumenta in modo progressivo mano mano che superiamo la zona di headroom mentre un segnale digitale passa repentinamente dalla riproduzione corretta (sotto lo 0 dBfs) alla distorsione (sopra lo 0 dBfs). Di seguito viene riportato il confronto fra la scala dBfs e la scala dBu, notiamo come 0 Vu cioè +4dBu corrispondano a -15 dBfs:
Standard Operating Level
Abbiamo detto che una catena audio è l'insieme degli stadi che un segnale audio attraversa per essere continuamente trasformato in ciò di cui abbiamo bisogno. Ogni stadio riceve in ingresso un segnale elettrico, lo manipola e restituisce in uscita il risultato della manipolazione che ha operato. Ciò che esce da questo stadio andrà verosimilmente all'ingresso di uno stadio successivo che opererà una nuova trasformazione e così via. Per fissare le idee possiamo immaginare che l'ultimo stadio che consideriamo sia un amplificatore di potenza collegato ad un sistema di altoparlanti.
Cosa succede se l'uscita di uno stadio risulta essere ad un voltaggio molto maggiore del voltaggio che lo stadio successivo è in grado di gestire?. La risposta non è immediata e comprende molti fattori, diremo per generalizzare che il secondo stadio si troverà a manipolare un segnale troppo alto per cui non è stato tarato.
Ciò porta all'introduzione di una distorsione di saturazione che sarà tanto maggiore quanto più il segnale sarà maggiore di quello che il secondo stadio si aspetta. Ma cosa si aspetta il secondo stadio? La risposta è nel SOL (Standard Operating Level), il livello standard di operatività. Per esempio possiamo dire che il SOL di un certo modulo è di 1Volt e con ciò intenderemo che il segnale audio che transita per quello stadio avrà valori massimi attorno a 1 Volt (in realtà il SOL viene misurato in dB) o di poco superiori. Ogni componente audio lavora ad un certo SOL e otterremo il massimo delle sue prestazioni facendolo interagire con altri componenti che lavorano allo stesso SOL.
Nella tabella seguente vengono riportati i valori del SOL e il corrispondente voltaggio nei diversi contesti di operatività:
| Contesto di operatività | dB | Volt |
|---|---|---|
| Professionale | +4 dBu | 1.2 V |
| Semi-Professionale | -10 dBv | 0.32 V |
| Broadcast | 6-8 dBu | 1.55 V-1.95 V |
| HiFi-Utente medio | -10 dBu | 0.25 V |
Osservando questa tabella si possono fare interessanti considerazioni. Intanto vediamo come ogni contesto abbia una sua misura in dB dei valori di riferimento (dBu in ambito professionale, semi-pro e broadcast, dBV in ambito
semi- rofessionale). Ma il vero dato interessante è la colonna dei voltaggi.
Vediamo come per ambito professionale il voltaggio relativo al SOL è 1.2V mentre nel campo HiFi è pari a 0.25V.
Il primo segnale ha un'ampiezza circa pari a 5 volte quella del secondo e dunque permette una riproduzione molto più fedele (per convincervi di questo fatto immaginate di lavorare con un SOL di 0.000001V, sareste ancora in grado di apprezzare una differenza tra due voltaggi del tipo: 0.0000015V e 0.0000016V ?). Dunque più è alto il SOL (più è alto il voltaggio a cui si lavora) più la riproduzione della forma d'onda è accurata. Ovviamente la qualità costa; circuiti che lavorano con voltaggi più alti sono più costosi.
Dynamic Range
Per dynamic range (dinamica)h si intende l'intervallo misurato in dB (quale dB poi varia a seconda del contesto di cui si sta considerando la dinamica) tra il valore minimo che il segnale audio può assumere e quello massimo. In natura i suoni hanno una certa dinamica. Un refolo di vento ha una dinamica piccola perché il suo valore massimo in dB non è molto superiore a quello che si ha in assenza di suono. La dinamica del suono generato da un uragano invece è molto più ampia.
Inoltre in natura è sempre presente un rumore di fondo che possiamo attestare, in un ambiente cittadino mediamente rumoroso, a circa 30dBspl.
Dunque suoni che producono un numero di dBspl inferiore a 30 possono essere trascurati nel senso che non vengono percepiti con chiarezza essendo mascherati dal rumore di fondo. Nel nostro generico esempio potremo considerare che la maggior parte dei suoni non va oltre i 100 dBspl e dunque assesteremo su questo valore il nostro SOL. Tuttavia può capitare che per brevi periodi vengano prodotti suoni di intensità maggiore, diciamo non oltre un valore massimo di 120 dBspl (valore che corrisponde approssimativamente alla soglia di dolore per l'orecchio umano). Nella parte a sinistra della figura sottostante possiamo vedere la scala con i valori che abbiamo fissato:

La differenza in dB tra il SOL e il rumore di fondo viene chiamata rapporto segnale rumore (SNR -Signal to Noise Ratio) e dà una misura di quanto un suono sia "più
forte" del rumore di fondo. La differenza in dB tra il valore massimo della dinamica e il SOL viene detta Headroom. La somma in dB tra l'Headroom e il SNR è il Dynamic Range (Per avere chiare queste grandezze riferirsi alla parte sinistra della figura precedente). Una volta definito questo insieme di valori in ambito fisico possiamo vederne l'equivalente elettrico (parte a destra della figura soprastante). Per prima cosa focalizziamo l'attenzione sul rumore. Qualsiasi apparato elettrico è affetto da rumore (per esempio il rumore termico dei componenti elettronici o il naturale fruscio di un nastro magnetico). Questa volta però si tratta di un rumore elettrico e dunque misurato in dBu e non più in dBspl, supponiamo di aver misurato un valore del rumore di fondo pari a -66dBu. Il nostro SOL, dato che vogliamo lavorare con attrezzature professionali, sarà +4dBu (equivalenti dei 100 dBspl) mentre come Headroom possiamo prendere 20 dBu per mantenere le proporzioni con il caso reale. Facendo un pò di conti otteniamo un SNR di 70dBu e dunque una dinamica di 90dBu. Con questi valori fissati saremmo sicuri di poter riprodurre correttamente qualsiasi suono compreso tra i valori di 30dBspl e 120dBspl cioè con una dinamica di 90dBspl. Se si pensa che i brani da discoteca vengono compressi fino ad arrivare ad avere una dinamica massima di 30dB capite che con 100dB di dinamica a disposizione si possono fare grandi cose.
Un valido esempio è la registrazione di un'orchestra. In questo caso infatti si va da valori molto bassi di dBspl nelle parti in cui sussurra un solo strumento a valori molto alti quando per esempio tutti gli strumenti suonano insieme in crescendo trionfale. Con 90dBu a disposizione è possibile registrare tutti questi suoni di intensità così diversa con la stessa fedeltà.
Un altro esempio è la registrazione di una voce che in un brano passa dal sussurro all'urlo. Generalmente si predispongono più microfoni e si settano i preamplificatori a valori diversi del SOL ognuno ottimizzato per una particolare intensità sonora. In fase di missaggio poi si combineranno le varie sezioni registrate in modo che la riproduzione sia fedele in tutte le parti del brano.
Ora capiamo anche meglio i valori della tabella del paragrafo precedente. Valori di SOL maggiori e dunque voltaggi più alti sono più lontani dal rumore di fondo e dunque consentono una dinamica maggiore.
Fenometri
Misuratori di dBspl
Generalmente vengono costruiti con all'interno un microfono molto sensibile e sono tarati per rilevare una pressione sonora con una risposta che riproduce quella
dell'orecchio umano.
Di solito è presente uno switch di taratura dell'apparecchio in relazione alla sorgente sonora da misurare, questo fa sì che venga attivato un circuito di misurazione piuttosto che un altro:
Circuito A: La curva di risposta del circuito corrisponde alla curva isofonica a 40 phons dell'orecchio umano [Curve Isofoniche] e consente misure accurate di pressioni sonore modeste come quelle generate nell'ambito di una normale conversazione.
Circuito B: La curva di risposta del circuito corrisponde alla curva a 70 phons dell'orecchio umano. È adatto a misure di pressioni sonore comprese tra i 55 e gli 85 dBspl.
Circuito C: Attiva un circuito con una curva di risposta piatta. È adatto a letture di valori maggiori di 85 dBspl. A volte è presente anche un circuito di tipo D adibito a misure di pressioni sonore molto elevate.
Vu Meters
Lo zero, nei Vu Meters indica sempre il SOL dunque per le apparecchiture professionali, indica +4dBu (1.2V) mentre sull'Hi-Fi di casa indica -10dBu (0.25V).
I Vu meters danno una misura del RMS del segnale ossia del suo valore efficace e vengono utilizzati per apparecchiature analogiche soprattutto sui registratori. Non sono fatti per visualizzare tutti i transienti del segnale data anche la massa inerziale degli indicatori.
PPM Meters
PPM stà per Peak Program Meter e come dice il nome fornisce una misura dei valori di picco del segnale e non del valore efficace. Inoltre il misuratore segue tutti i transienti del segnale e viene impiegato soprattutto per misure su segnali digitali. L'unità di misura è il dBfs (Full Scale).