
IL SUONO
Cos'è il suono
Una prima definizione che possiamo dare è che quello che noi percepiamo come suono è una variazione, rispetto ad un valore costante, nella pressione dell'aria.
Quando questa variazione viene ripetuta ciclicamente un certo numero di volte in un intervallo di tempo, che definiremo meglio in seguito, percepiamo un suono.
Affinchè un suono si possa propagare ha bisogno di un mezzo che lo trasporti;
l'aria è uno di questi in quanto le sue particelle, come vedremo, si trasmettono l'un l'altra la vibrazione generata dalla sorgente sonora e la propagano nello spazio. Questo significa che qualsiasi mezzo, solido, liquido o gassoso che sia, è in grado di trasportare il suono, influendo sulla sua velocità a seconda della sua densità.
Come mezzo di riferimento per i nostri esempi considereremo l'aria essendo quello con cui avremo a che fare nei casi pratici.
Il suono si propaga nell'aria mediante collisioni multiple tra particelle.
Consideriamo di avere un altoparlante e sia questo la nostra sorgente sonora.
Il cono si muove avanti e indietro seguendo l'ampiezza del segnale elettrico che viene applicato all'induttore su cui si appoggia.
Così facendo sposta delle particelle d'aria comprimendole prima e dilatandole poi. Seguiamo la propagazione del suono a partire dalla sorgente sonora (l'altoparlante), per fissare le idee supporremo che prima avvenga una
compressione verso destra, poi una dilatazione verso sinistra:
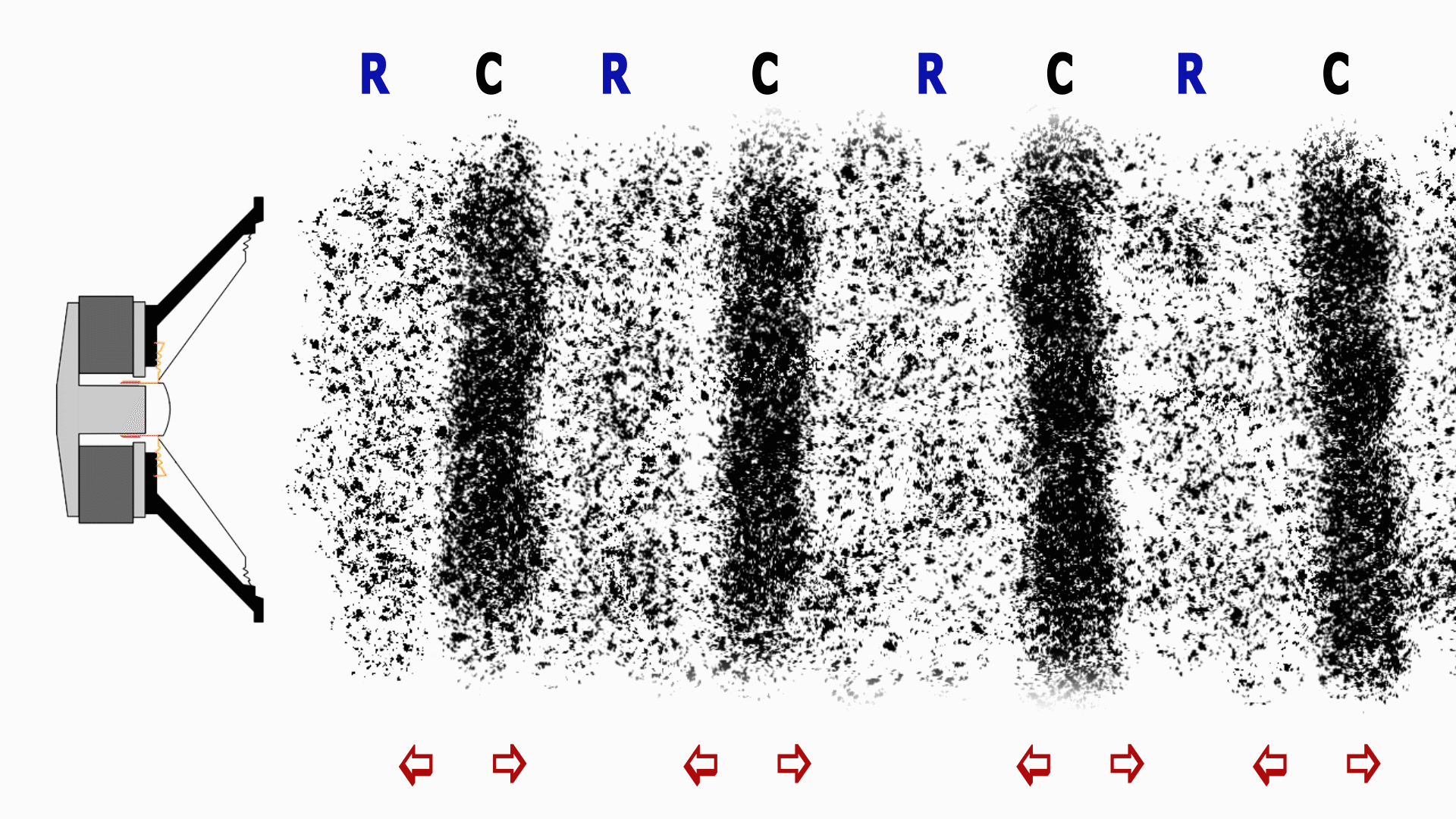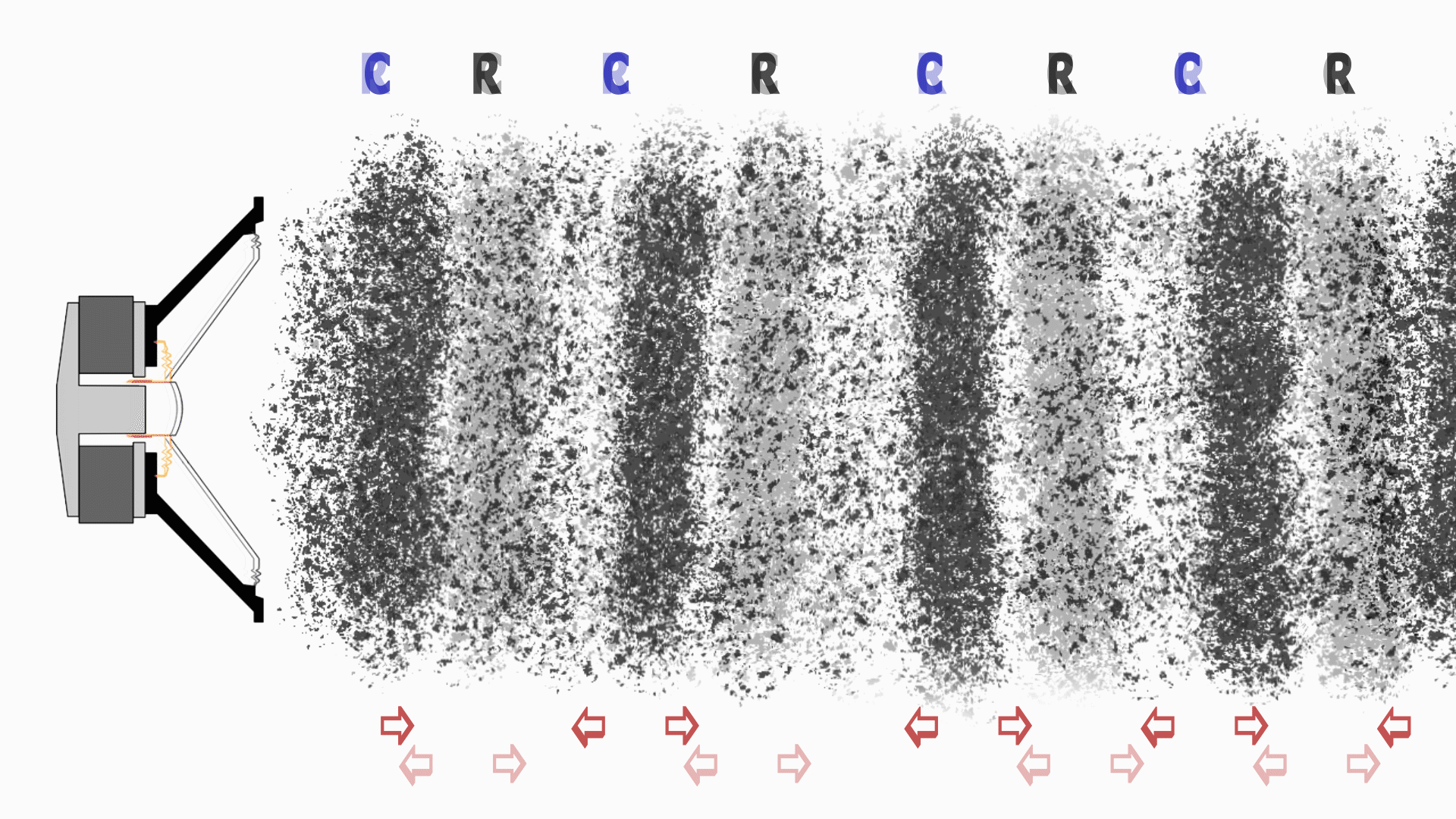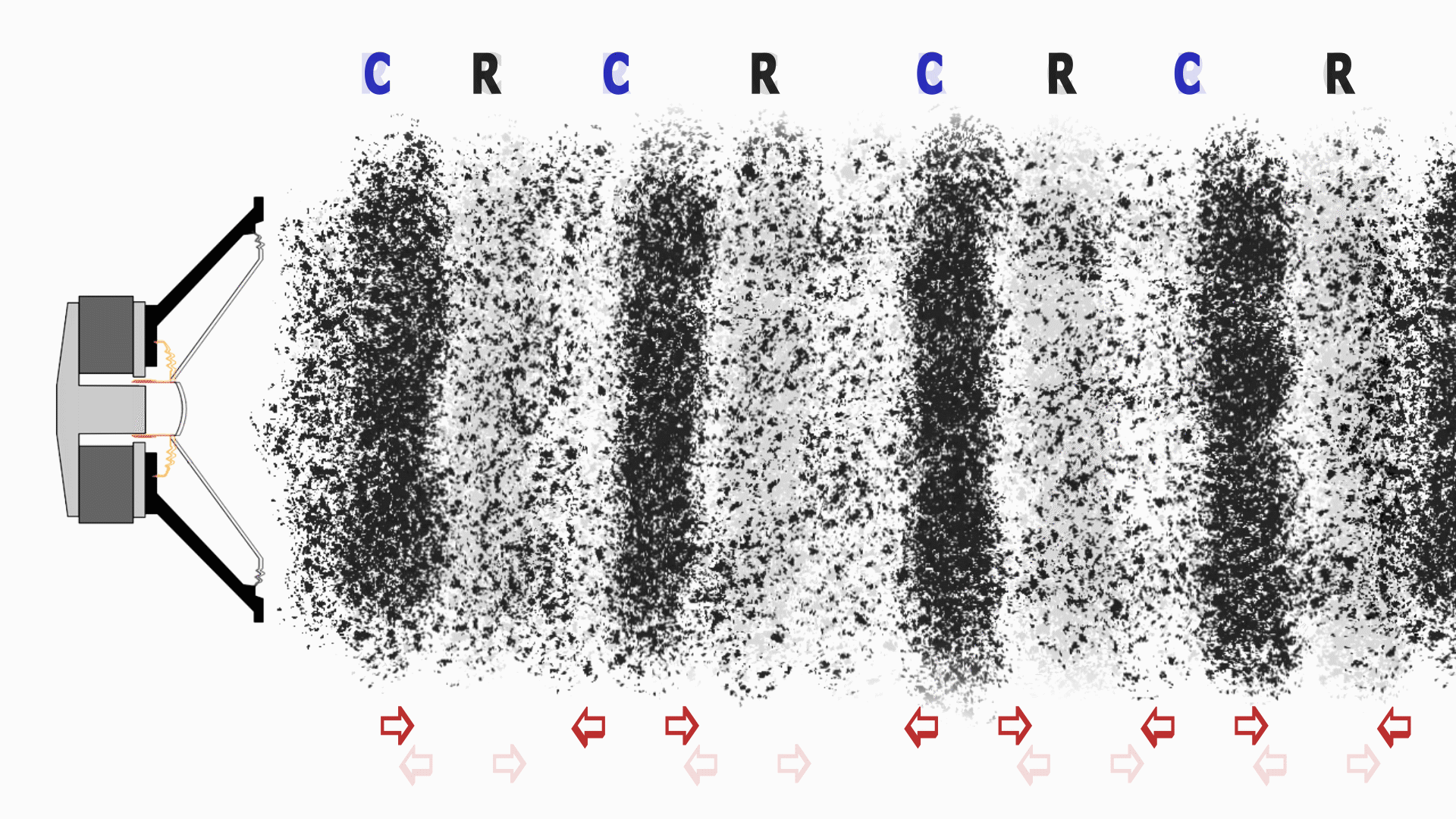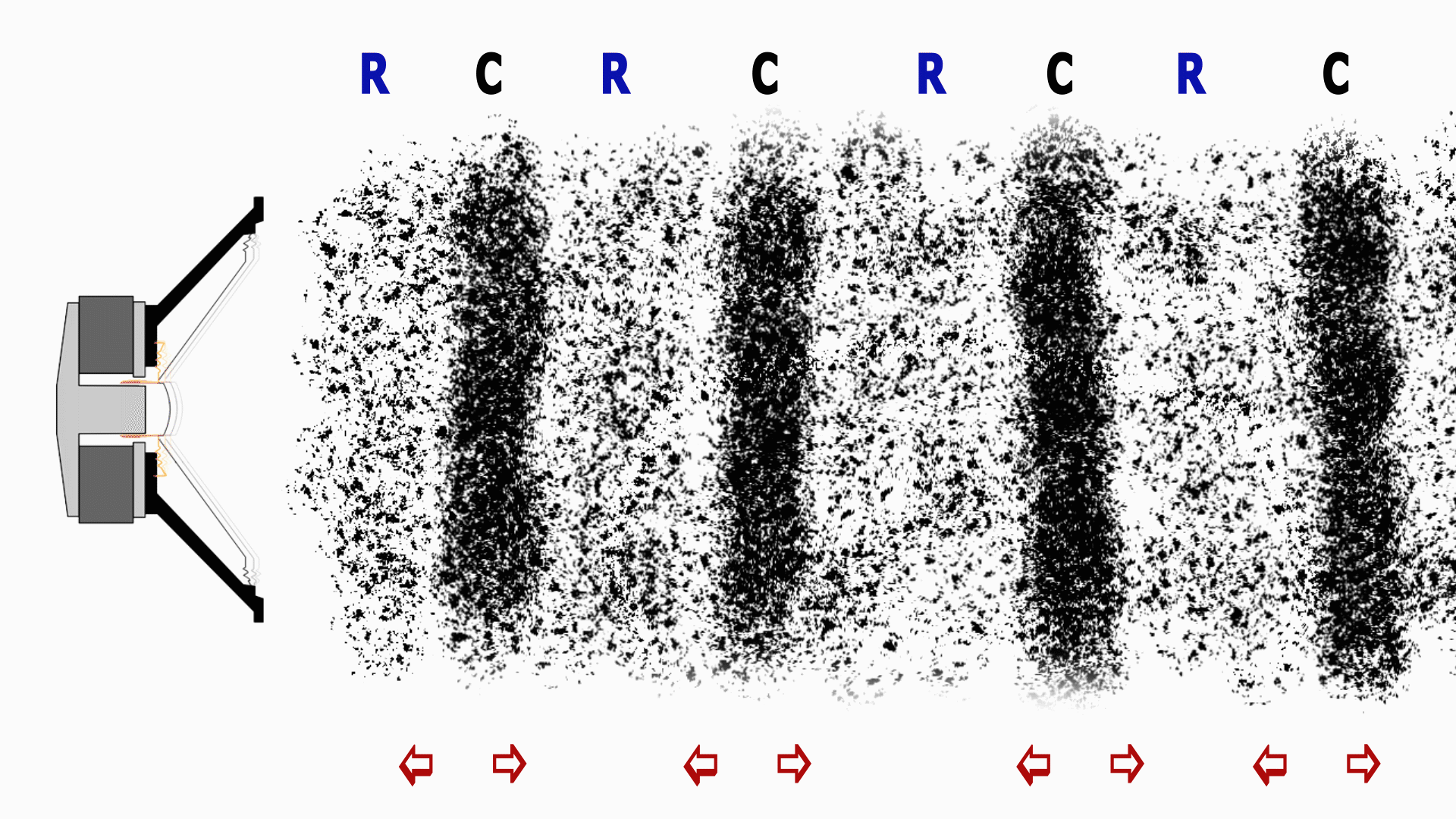
C=Compression "Compressione"
R=Rarefaction "Dilatazione"
L'altoparlante si muove e spinge le particelle d'aria che si trovano alla sua destra (fase a) operando una compressione.
Queste, a loro volta vanno a spingere le particelle che sono a loro vicine e trasferiscono loro l'energia che hanno ricevuto l'altoparlante.
In seguito l'altoparlante torna indietro ed esegue una compressione nel verso opposto ovvero una dilatazione verso sinistra (fase b) e nel fare ciò crea una depressione davanti a se che viene colmata dalle particelle d'aria che si trovano nelle immediate vicinanze.
Queste particelle che si muovono creano a loro volta una depressione alla loro destra e così via.
Questo procedimento fa sì che la particelle trasmettano l'energia oscillando e non muovendosi fisicamente nella direzione di propagazione del suono.
Le forme d'onda possono arrivare ad essere molto complicate ma per fortuna, tutte le onde possono essere considerate come un'estensione di una forma d'onda molto semplice; la sinusoide, espressa nella sua forma più generica dalla seguente formula:
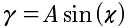
La figura seguente mostra il grafico di una sinusoide:
La sinusoide ha una serie di proprietà:
Frequenza (f)
Periodo (T)
Lunghezza d'onda (λ)
Ampiezza (A)
Fase (φ)
Velocità (v)
La frequenza è il numero di cicli che vengono compiuti dall'onda in un secondo dove un ciclo si intende composto da una semionda positiva e una semionda negativa.
Viene misurata in Hz[1/sec], un'onda di frequenza pari a 1Hz
compie un ciclo ogni secondo. La figura seguente mostra una sinusoide di
frequenza pari a 2 Hz:

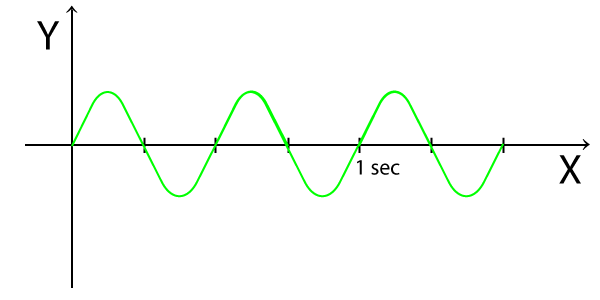
Il periodo è il tempo impiegato per compiere un ciclo completo.
La figura seguente mostra la durata del periodo di una sinusoide con il suo valore:
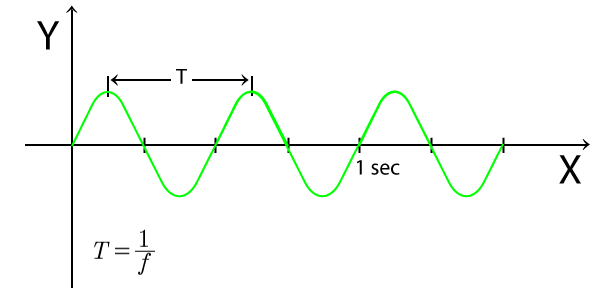
La lunghezza d'onda definita come la distanza tra due punti corrispondenti lungo la forma d'onda.
Il suo valore può essere calcolato a partire dalla formula seguente:
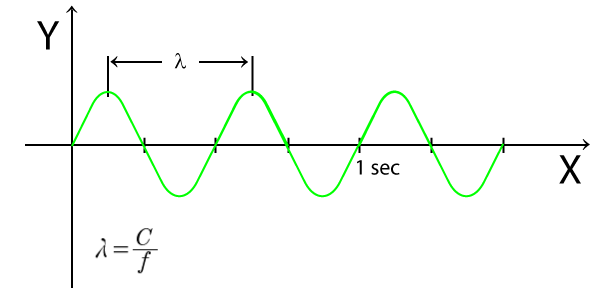
Dove:
c = velocità del suono, consideriamo nel nostro caso (l'aria ed è 344 m/sec).
Per cominciare ad avere un'idea delle dimensioni che vengono tirate in ballo possiamo considerare un'onda di frequenza 1Hz che viaggia nell'aria.
Per la formula che si trova nell'immagine avremo che:
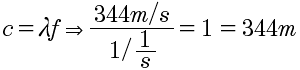
Calcolo della velocità del suono
Cioè ogni ciclo l'onda si estende per 344 m...!!
Come vedremo l'orecchio umano comincia a percepire suoni di frequenza superiore ai 20-30Hz quindi lunghezze d'onda di 15-18 metri.
L' ampiezza è la misura dello scostamento massimo dalla posizione di equilibrio.
Ampiezze maggiori corrispondono a volumi più alti.
Esistono due tipi misura delle ampiezze.La prima è una misura di tipo assoluto ed è detta ampiezza di picco.
Questa misura effettivamente il punto in cui si l'onda ha ampiezza massima.
La seconda è una misura sull'ampiezza come viene percepita dall'orecchio.
Si parla in questo caso di ampiezza efficace (RMS, Root Mean Square), la formula è nel grafico:
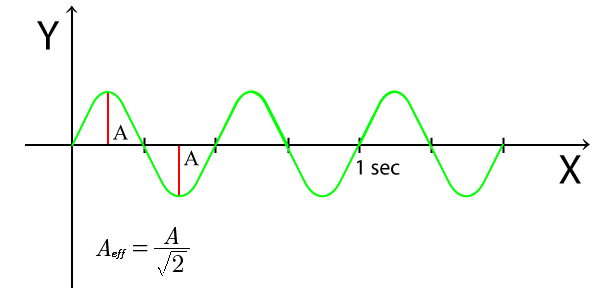
La fase, questa grandezza è sempre una relazione tra due forme d'onda.
Per capire questo concetto occorre spiegare come viene costruita una forma d'onda sinusoidale.
Per fare ciò faremo riferimento alla figura seguente:
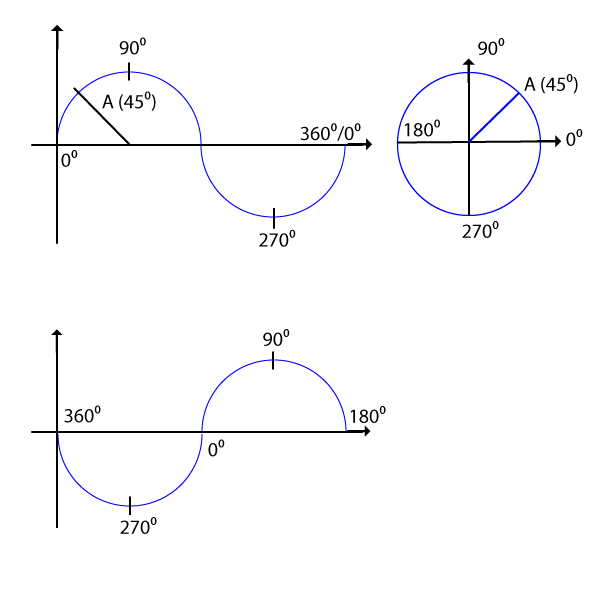
Immaginiamo che il punto A si muova lungo la circonferenza in senso antiorario a partire dal punto a 0 gradi. Se α è l'angolo avremo che i segmenti proiezione del punto A sugli assi x e y saranno rispettivamente:
y = sin(α )
x = cos(α )
Quindi quello che vedete nel grafico (a) non è altro che la lunghezza della proiezione del punto A sull'asse delle ordinate (y) al variare dell'angolo.
Immaginate ora di far ruotare il punto A in senso orario, la sua proiezione sulle y sarà all'inizio negativa e avrà l'andamento della figura (b).
Ora possiamo dare un'altra interpretazione della frequenza dicendo che sarà il numero di volte che il punto A compie un giro completo in un secondo.
L'ampiezza massima si avrà sempre a 90o indipendentemente dalla frequenza, più in generale possiamo dire che la fase non dipende dalla frequenza.
L'equazione che lega la fase al tempo è:
Il legame tra ritardo e fase, per dare un esempio della sua utilità possiamo calcolare il ritardo necessario affinchè due sinusoidi di frequenza 100Hz arrivino sfasate di 90o:
Sostituiamo i valori nell'equazione e risolviamo:
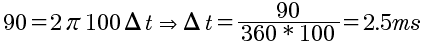
Calcolo del ritardo tra due sinusoidi
La velocità:
Si è accennato che la velocità del suono nell'aria è di circa 344m/s.
Più il mezzo è denso, più il suono si propaga velocemente e vedremo meglio nel seguito come questo fatto sia alla base del fenomeno della rifrazione [Rifrazione] . Un suono che si propaga all'interno di un mezzo ha una velocità di propagazione che dipende dalle caratteristiche del mezzo stesso.
Ogni mezzo ha una sua tipica velocità del suono calcolata ad una temperatura costante di 23.24 oC.
Questo serve come valore di riferimento in quanto al variare della temperatura, variano le caratteristiche del mezzo e dunque la velocità del suono al suo interno. Quando un mezzo viene riscaldato, alle sue particelle viene trasferita energia cinetica.
Quando vengono in contatto con un fronte d'onda, le particelle del mezzo rispondono più prontamente alla sollecitazione e trasmettono dunque l'energia sonora ricevuta più velocemente.
Ciò si traduce nella maggiore velocità del suono nel mezzo.
Mediamente si riscontra un aumento (diminuzione) di velocità di 0.6 m/s per ogni incremento (decremento) di un grado C della temperatura del mezzo.
Combinazione di sinusoidi pure
La sinusoide è la forma d'onda più semplice che possiamo immaginare, e come tale anche la meno interessante dal punto di vista dell'estetica del suono.
Si è detto di come qualsiasi forma d'onda sia riconducibile ad una combinazione (somma) di sinusoidi con opportuna ampiezza e fase.
Questa è stata la straordinaria scoperta fatta dal matematico francese Jean Baptiste Fourier (1768 - 1830)
Comunque, partiamo dal principio.
Prendiamo due forme d'onda in fase. Se ricordate l'esempio del puntino che gira lungo la circonferenza in senso antiorario pensate a due forme d'onda generate da due punti che partono allo stesso istante e vanno alla stessa velocità:
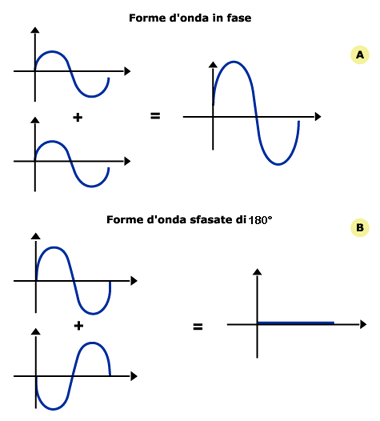
Somma e differenza di sinusoidi
Vediamo che la somma delle due è una sinusoide di ampiezza doppia rispetto alle due precedenti.
A livello di audio che succede? Sentiamo un suono alla stessa frequenza delle due onde componenti ma l'ampiezza doppia fa si che il volume sia più alto.
Di quanto?
Non del doppio, un pò meno ma di questo parleremo più avanti.
Cosa succede se sommiamo due forme d'onda in controfase (pensate ai soliti due punti, uno girerà in senso orario, l'altro in senso antiorario)? Non avete bisogno di una risposta...
Ancora troppo semplice? Va bene, prendiamo due forme d'onda sfasate di 90 gradi con diversa frequenza (una doppia dell'altra).
Il suono seguente consiste in una sinusoide di frequenza pari a 1 KHz e una fase
di 0o:
Sinusoide [f=1KHz, ϕ=0o]
Il suono seguente invece consiste in una sinusoide di frequenza doppia rispetto alla precedente, ossia pari a 2 KHz, e avente una fase iniziale di 90o:
Sinusoide [f=2KHz, ϕ=90o]
I grafici delle due forme d'onda sono confrontati nella figura seguente:
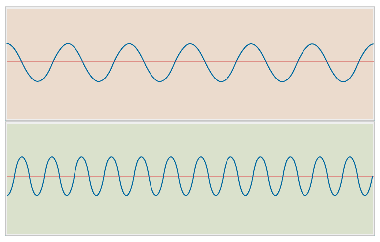
Come detto, una caratteristica dei suoni è che possono essere sommati senza interferire l'uno con l'altro. Sommando i due suoni precedenti otteniamo un nuovo suono in cui è possibile distinguere chiaramente le due componenti sommate:
Sinusoide somma di 1 KHz (0o)+ 2 KHz (90o)
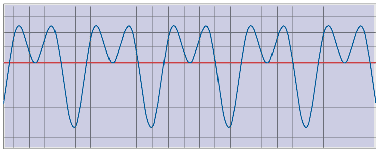
Rappresentazione tempo - frequenza
Questa è forse la parte più importante per capire a fondo la natura di un suono. La trattazione matematica di questo argomento può diventare molto complessa, qui ci basterà accennare ai dettami fondamentali tralasciando i rigori imposti dalla divulgazione scientifica.
I grafici che abbiamo visto finora erano del tipo Ampiezza-Tempo ossia descrivevano l'andamento dell'ampiezza al variare del tempo. Consideriamo ora un diverso approccio alla questione e vediamo come sia possibile rappresentare l'ampiezza in funzione della frequenza.
Nel caso di una sinusoide pura di equazione y=A sin(2πft) possiamo senz'altro dire che sia la frequenza f che l'ampiezza A sono costanti. E allora in un diagramma Ampiezza-Frequenza, una sinusoide di ampiezza A e frequenza f la rappresentiamo come in figura mentre le due sinusoidi del'esempio precedente avranno una rappresentazione come nella figura che segue:
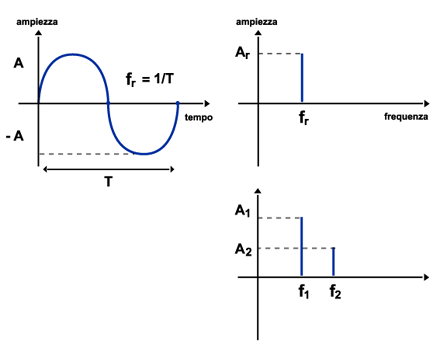
Dunque una sinusoide è rappresentabile, in un diagramma Ampiezza-Frequenza, come un segmento di lunghezza pari all'ampiezza della sinusoide e posizionata sulla sua frequenza (questa frase farebbe inorridire qualsiasi fisico ma come già detto in questa sede non siamo interessati ai rigori scientifici quanto piuttosto alla comprensione generale dei fenomeni).
Ora mettiamo insieme tutte queste cose. Immaginiamo un suono complesso cioè composto da tutte le sinusoidi da 20Hz a 20KHz ( questo è più o meno l'intervallo delle frequenze udibili dall'orecchio umano, quindi dal nostro punto di vista sono le uniche frequenze che ci interessano).
Consideriamo un segnale sonoro complesso come quello mostrato nella figura seguente
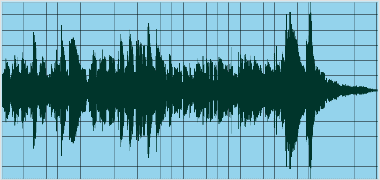
Il suo spettro di frequenza varierà continuamente nel tempo e se immaginiamo di 'fotografare' lo spettro in un determinato istante avremo su un diagramma Ampiezza-Frequenza il seguente tipo di grafico:
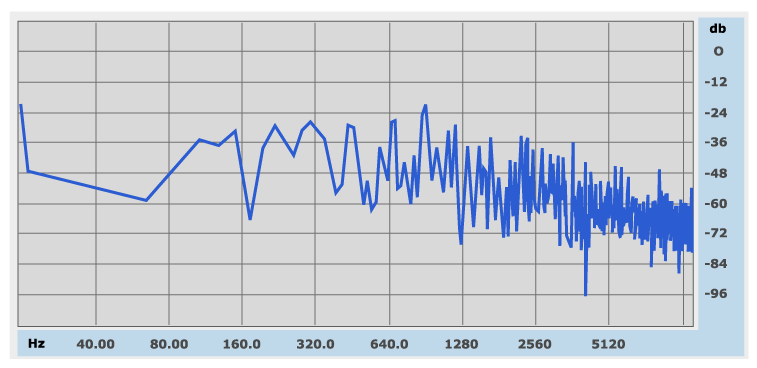
Un suono non sta mai fermo ma varia continuamente nel tempo. Ciò significa che ogni sinusoide componente varia la sua ampiezza e dunque varia anche la forma del grafico dello spettro. Questo spiega cosa si vede quando si osserva un analizzatore di spettro con tutti quei LED che sembrano impazziti. Vi sta mostrando l'ampiezza delle sinusoidi. Questo spiega anche cosa fa un equalizzatore grafico [Equalizzatore grafico] , amplifica o attenua (aumenta o diminuisce) l'ampiezza delle sinusoidi. L'intervallo 20Hz-20KHz è un intervallo continuo quindi in un equalizzatore ogni cursore controlla una banda di frequenze, più aumentano i cursori più le bande sono strette, nel caso ideale di infiniti cursori, ogni cursore controlla l'ampiezza di una singola frequenza o meglio della sinusoide a quella frequenza.
Contenuto armonico di una forma d'onda
Quanto detto finora è riferito alla sinusoide come tassello fondamentale per mezzo del quale costruire il resto della realtà sonora. Un aspetto che contribuisce non poco a caratterizzare un suono sono le sue armoniche. Per illustrare questo concetto conviene riferirsi ad un caso pratico anche per cominciare un pò ad uscire dalle trattazioni puramente teoriche e cominciare a vedere in pratica cosa significhino questi discorsi. Consideriamo allora cosa succede quando la quinta corda di una chitarra viene pizzicata da un chitarrista. Diremo tutti che il chitarrista sta eseguendo un La ma fisicamente, cosa succede?
La corda si è messa ad oscillare ad una frequenza di 440Hz. Ma allora com'è che non suona come una semplice sinusoide di frequenza pari a quella ma suona con il suono di una chitarra? La risposta comprende una serie di ragioni che si chiariranno via via. Sicuramente il contenuto armonico della nota suonata dal chitarrista non è uguale a quello di una semplice sinusoide. Quando una nota viene suonata su uno strumento viene sicuramente generata la frequenza corrispondente alla nota che viene chiamata armonica fondamentale e insieme a questa vengono generate le armoniche cioè tutti i multipli interi di quella frequenza con ampiezza via via decrescente. Nel caso del La vengono generate le sinusoidi:
▶ 880 Hz Seconda Armonica
▶1320 Hz Terza Armonica
▶ ... ... ...
▶n*440 Hz n-esima Armonica
Questo comportamento deriva dal fatto che la corda pizzicata dal chitarrista non
oscilla solo alla frequenza fondamentale ma anche alle frequenze armoniche secondo la figura seguente:
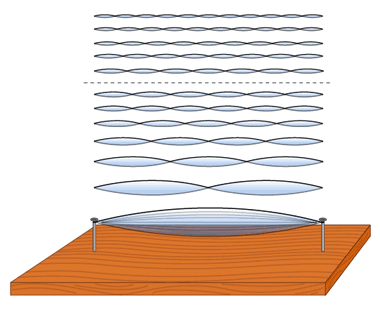
Oscillazioni armoniche di una corda in vibrazione
La prima armonica è detta anche fondamentale e caratterizza la nota che effettivamente percepiamo, notiamo che è quella che ha ampiezza maggiore. La seconda armonica è ad una frequenza doppia rispetto alla fondamentale, ciò significa che la corda sta vibrando come in figura sovrapponendo questa vibrazione a quella fondamentale.
Se state leggendo questo testo non dovreste essere completamente digiuni di nozioni musicali e dunque dovreste sapere che quando si aggiunge un'ottava ad una nota si ritrova la stessa nota di partenza, nel nostro caso un La (ovviamente più acuta, se non siete convinti di questo provatelo su un pianoforte). Dunque la seconda armonica è la stessa nota della fondamentale e aggiunge calore al suono. La terza armonica non è più un La e dunque contribuisce ad arricchire il suono.
Dalla figura potete vedere come vengano generate le armoniche successive e notare come l'ampiezza di queste diminuisca all'aumentare della frequenza dell'armonica. In altre parole, se una corda di chitarra viene pizzicata, le armoniche che contribuiscono al suono in modo rilevante sono una decina. Le ampiezze delle armoniche successive rispetto all'ampiezza della fondamentale diventano trascurabili. Si può notare anche come al centro della corda si abbia una prevalenza di basse frequenze mentre ai lati prevalgano le alte. Questo è molto importante per esempio nel piazzamento dei microfoni: se dal rullante di una batteria volessimo un suono composto da alte frequenze punteremo il microfono verso il bordo mentre se volessimo un suono in cui prevalgano i bassi punteremo il microfono verso il centro.
Gli amplificatori per chitarra possono essere valvolari o a transistor e troverete sostenitori accaniti sia del primo che del secondo tipo a causa del diverso suono che essi generano. I transistor tendono ad enfatizzare la terza armonica mentre le valvole enfatizzano la seconda e ora potete capire perchè questo influisca in modo così sostanziale sul suono.
Forme d'onda
Sinusoide pura: È stata ampiamente descritta nei paragrafi precedenti. Viene percepita come un tono di frequenza pari alla frequenza della sinusoide. È facilmente generabile elettronicamente e viene spesso usata come strumento di test.
Nei paragrafi precedenti sono stati già illustrati l'andamento e il suono prodotto nonché le diverse proprietà che la caratterizzano
L'onda quadra si presenta come in figura:
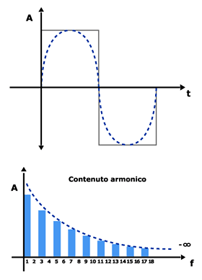
Onda quadra (f = 440 Hz)
Ondo quadra (f = 1 KHz)
Come vediamo, il contenuto armonico dell'onda quadra è composto dalle sole armoniche dispari.
L'ampiezza decresce con un andamento di tipo 1/f. Questo in via empirica significa che la seconda armonica (quella che ha frequenza tripla della fondamentale, quella a frequenza doppia non è presente) ha ampiezza pari a 1/3 della fondamentale, la terza pari a 1/5 e così via.
Di seguito vengono presentati i suoni di un'onda quadra, una alla frequenza di 440 Hz (equivalente alla nota musicale La) e una alla frequenza di 1 KHz:
Onda a dente di sega
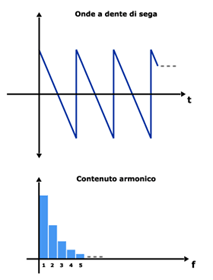
Nell'onda a dente di sega sono presenti tutte le armoniche, l'ampiezza di ogni armonica è pari alla metà dell'armonica precedente.
Di seguito vengono presentati i suoni di un'onda a dente di sega, una alla frequenza di 440 Hz (equivalente alla nota musicale La) e una alla frequenza di 1 KHz:
Ondo dente di sega (f = 1 KHz)
Ondo denta di sega (f = 1 KHz)
Onda triangolare
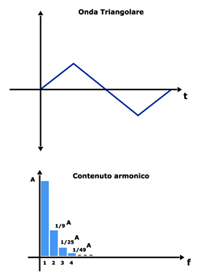
Ha un contenuto armonico molto simile a quello dell'onda quadra. La differenza è che le ampiezze decrescono con un andamento del tipo 1 / f2.
Di seguito vengono presentati i suoni di un'onda triangolare, una alla frequenza di 440 Hz (equivalente alla nota musicale La) e una alla frequenza di 1 KHz
Ondo triangolare (f = 1 KHz)
Ondo triangolare (f = 1 KHz)
Ipertoni
La differenza fondamentale con le armoniche è che gli ipertoni non hanno nessuna relazione con la frequenza fondamentale mentre le armoniche sono multiple di questa.
Gli ipertoni dipendono fortemente dallo strumento che li ha generati e contribuiscono a caratterizzare il suono anche se hanno ampiezza minore delle armoniche.
Inviluppo del suono
Con questo termine si intende l'andamento dell'ampiezza di un suono dal momento in cui viene generato a quando si estingue. Per introdurre questo concetto conviene considerare un esempio pratico. Il più eloquente è quello di uno strumento a corda, per esempio una chitarra.
Dunque quando il chitarrista esegue una nota, percepiamo un primo impatto sonoro, poi piano piano la nota si estingue. L'andamento dell'ampiezza della nota suonata viene chiamato inviluppo ADRS (acronimo delle parole:Attack, Decay, Sustain, Release.
Ha uno schema che può essere applicato a qualsiasi suono e strumento.
Descriviamo le quattro fasi nel dettaglio:
Decay: Dopo l'attacco, parte dell'energia iniziale viene persa e l'ampiezza diminuisce.
Sustain: L'ampiezza mantiene un livello quasi costante per un certo tempo.
Release: L'ampiezza ricomincia a diminuire fino ad annullarsi.
Di seguito vediamo un esempio di inviluppo ADSR la forma d'onda di un suono viene circoscritta da una curva che descrive l'andamento dell'ampiezza e che in matmatica prende il nome di inviluppo. Data la simmetria della forma d'onda, se ne considera, ai fini della valutazione dell'inviluppo, la sola parte positiva
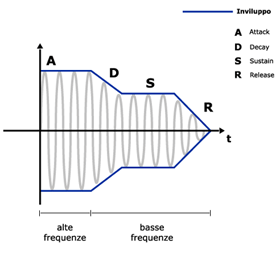
Nella figura viene anche evidenziato il fatto che la parte iniziale del suono ha un maggior contenuto di alte frequenze che sono poi le prime ad estinguersi. Generalmente nella fase di sustain il contenuto di alte frequenze si è attenuato mentre continuano ad essere presenti le basse frequenze.
Di seguito viene riportato il suono generato dalla quinta corda di una chitarra acustica (La) e la sua visualizzazione in tempo.
Nota La suonata da chitarra acustica
Si può individuare abbastanza facilmente l'inviluppo ADSR.
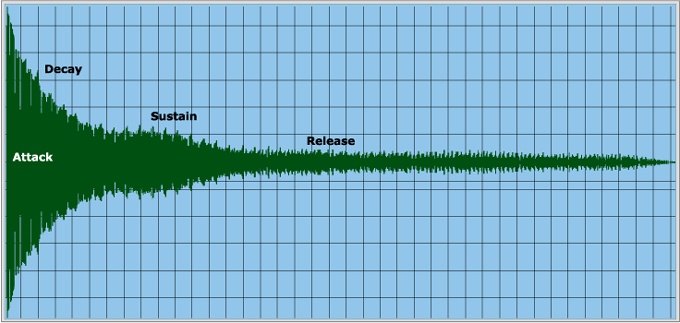
Come detto questo schema è applicabile alla maggior parte degli strumenti musicali e dei suoni in generale, ciò che varia è la durata della varie fasi. Per esempio, un rullante avrà tempi di Attack e Decay molto brevi. Un violino sarà contraddistinto da una fase Attack-Decay molto più lunga.
Generalmente la fase Attack-Decay è la più importante per caratterizzare un suono tanto che nelle moderne tecniche di sintesi si preferisce generare la parte Attack-Decay con dei campioni reali dello strumento da riprodurre e generare la parte di Sustain e Release in modo sintetico.
Questo ha un doppio obbiettivo. Da una parte fare sì che lo strumento sintetico somigli il più possibile a quello reale e dall'altra avere un controllo sulle caratteristiche dello stesso.
Per esempio una simulazione di vibrato è ottenibile in modo molto semplice su un suono sintetico mentre risulta un'operazione abbastanza complicata da realizzare su un suono campionato.
Comportamento del suono
In questa sezione viene descritto il comportamento del suono quando interagisce con degli ostacoli. Generalmente il materiale di cui è composto l'ostacolo e le sue dimensioni condizionano la natura dell'interazione al pari del contenuto di frequenze del suono che si sta considerando.
I comportamenti che verranno presi in esame valgono per le onde in generale anche se noi le contestualizzeremo all'ambito del suono. Analizzeremo nell'ordine:
2. Diffrazione
3. Rifrazione
4. Assorbimento
Riflessione
Prendiamo come riferimento la figura in cui viene mostrata un'onda (sonora) che incide su una superficie e viene riflessa. È importante avere ben presente che i fronti d'onda generati dalle compressioni e dalle dilatazioni sono perpendicolari alla direzione di propagazione dell'onda:
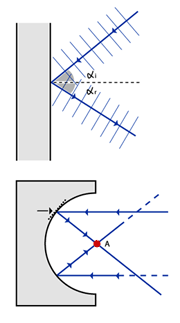
Un'onda che incide su una superficie piana con un angolo di incidenza α (tra la normale alla superficie e la direzione di propagazione dell'onda) viene riflessa con un angolo di riflessione pari ad α. In figura vediamo il caso di una superficie piana e quello di una superficie concava in cui tutti i raggi riflessi convergono verso il fuoco della superficie curva (per saperne di più sul fuoco rimandiamo a qualsiasi testo di geometria, qui basterà dire che in una circonferenza o in una sfera se pensiamo in 3D il fuoco coincide con il centro). Le superfici concave vengono evitate in acustica in quanto tendono a concentrare il suono in un preciso punto creando distribuzioni sonore disomogenee. Vengono invece utilizzate per la costruzione di microfoni direzionali in quanto consentono di amplificare segnali anche molto deboli.
Viceversa le superfici convesse hanno la proprietà di diffondere il suono e dunque sono ampiamente usate per migliorare l'acustica degli ambienti. Quando un'onda che si riflette su una superficie convessa, il prolungamento dell'onda riflessa passa per il fuoco della superficie.
Riflessioni all'interno di una stanza
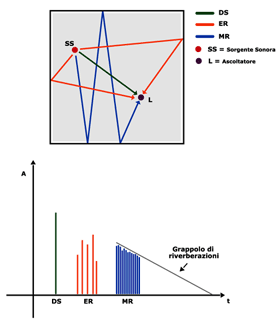
Quando un suono si propaga in una stanza, di cui abbiamo rappresentato una sezione vista dall'alto nella figura precedente, raggiunge l'ascoltatore in diversi modi. Il primo segnale che arriva all'ascoltatore è anche il più forte ed è quello diretto ossia quello che compie il percorso minore tra sorgente sonora e ascoltatore. Dopo il segnale diretto arrivano, con un breve sfasamento, i segnali che hanno subito una sola riflessione su una parete e dunque hanno ampiezza minore rispetto al segnale diretto a causa della perdita parziale di energia dovuta alla riflessione. Chiamiamo tali segnali prime riflessioni ('suono precoce' in alcuni testi). Dopo un ulteriore ritardo arrivano tutti i segnali che hanno subito più di una riflessione, di ampiezza ancora minore rispetto alle prime riflessioni. Questi vengono chiamati grappolo di riverberazione ('reverb cluster') a indicare che questi segnali non vanno considerati singolarmente ma piuttosto come un corpo unico. La figura seguente ci mostra la distribuzione di questi segnali nel tempo e le loro ampiezze.
Rifrazione
Con tale termine si indica il fenomeno secondo il quale un'onda che attraversa due mezzi di diversa densità cambia direzione nel passaggio dall'uno all'altro. Tale comportamento è facilmente spiegabile se teniamo presente ciò che abbiamo detto sulla velocità del suono in mezzi di diversa densità.
Sappiamo che il suono viaggia più velocemente in mezzi più densi. Consideriamo un'onda che incide contro un muro come è schematizzato dalla seguente figura:
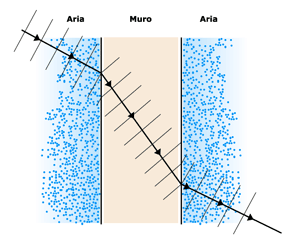
Il muro ha densità maggiore dell'aria dunque i fronti d'onda che cominciano a penetrare nel muro sono più veloci rispetto a quelli che ancora sono fuori. Dunque, all'entrata nel muro lo stesso fronte d'onda ha una parte più avanzata (quella interna al muro) e una più arretrata ( quella ancora esterna). Quando tutto il fronte d'onda è penetrato nel muro la direzione di propagazione ha cambiato angolo. All'uscita dal muro avviene lo stesso fenomeno all'inverso e l'onda torna alla sua direzione originaria. Di seguito vediamo come questo fenomeno diventi rilevante nel caso di concerti all'aperto dove le condizioni cambiano radicalmente dalla mattina alla sera modificando la propagazione del suono nell'ambiente.
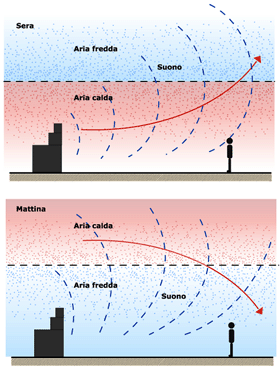
Rifrazione all'aperto
Alla mattina si verifica che lo strato superiore (aria fredda) abbia maggiore densità rispetto allo strato inferiore (aria calda) e dunque che il suono tenda a deviare verso l'alto come mostrato nella prima delle due figure precedenti.
Di sera la situazione si inverte e lo strato più denso (aria fredda) diventa quello inferiore. Ciò porta il suono a deviare verso il basso come evidenziato nella seconda delle due figure precedenti. Ciò va tenuto in conto durante la messa a punto di un concerto all'aperto [Suono live] in quanto la lunga fase di preparazione e test viene fatta molte ore prima dell'inizio del concerto stesso e dunque in situazioni ambientali che si modificano con il passare delle ore.
Diffrazione
Il modo più immediato ma efficace per descrivere questo fenomeno è dire che si verifica quando un suono aggira un ostacolo. Ciò dipende fortemente dalla frequenza in quanto suoni con una grande lunghezza d'onda (e dunque bassa frequenza) superano con facilità ostacoli con una dimensione minore della loro lunghezza d'onda.
Questo è uno dei motivi per cui le prime frequenze che vengono attenuate sono quelle alte mentre quelle basse si propagano a distanze molto maggiori.
Assorbimento
Puo` essere descritto come la conversione di energia acustica in energia termica da parte di una superficie. In altre parole, quando un suono viene a contatto con un ostacolo, gli trasferisce energia che viene dissipata sotto forma di calore.
In generale questi quattro fenomeni sono tutti presenti nel momento in cui un'onda sonora incontra un ostacolo. La figura seguente illustra una situazione tipica:
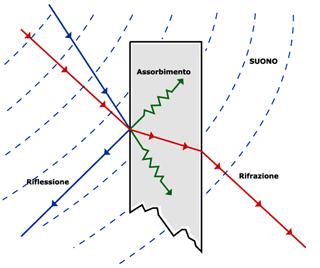
Riflessione, diffusione, rifrazione e assorbimento insieme